close
Categories
Blogs
Degree Programs

Business & Management

MBA in Supply Chain MBA in HR MBA in Marketing MBA in Healthcare Management Accelerated MBA

Nursing & Healthcare

Doctorate Master Bachelor Associate Affordable

Education & Teaching

Associate Affordable Doctorate Bachelor Master

Criminal Justice & Legal

Associate Master Doctorate Bachelor

Psychology & Counseling

Bachelor Master Associate Doctorate Affordable

Computers & Technology

Associate Bachelor Affordable Master
close
Home Categories Linear Regression

General Linear Models: Design of Experiments faq

instructor Instructor: statisticsmatt instructor-icon
duration Duration: 22.00 duration-icon

This course introduces the design of experiments and the use of general linear models. It covers topics such as projection matrices onto c(X), least square estimator of Beta, and estimability. It provides examples and explanations to help students understand the concepts and apply them to their own experiments. ▼▲

ADVERTISEMENT

Course Feature Course Overview Course Provider Discussion and Reviews
Go to class

Course Feature

costCost:

Free

providerProvider:

Youtube

certificateCertificate:

Paid Certification

languageLanguage:

English

start dateStart Date:

On-Demand

Course Overview

❗The content presented here is sourced directly from Youtube platform. For comprehensive course details, including enrollment information, simply click on the 'Go to class' link on our website.

Updated in [February 21st, 2023]


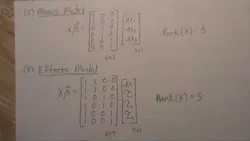
Design of Experiments: Models Introduction.
Design of Experiments: Projection Matrix onto c(X).
Design of Experiments: Projection Matrix onto c(X) Example.
Design of Experiments: Least Square Estimator of Beta.
Estimability (part 1/4): Necessary and Sufficient Conditions.
Estimability (part 2/4): Unique Unbiased Estimator.
Estimability (part 3/4): Gauss Markov Theorem.
Estimability (part 4/4): Generating Estimable Functions.
Design of Experiments: Estimating the Error Variance.
1-way fixed-effects ANOVA (part 1/10): Model Development.
1-way fixed-effects ANOVA (part 1/10): (Example) Model Development.
1-way fixed-effects ANOVA (part 2/10): Estimating Parameters.
1-way fixed-effects ANOVA (part 2/10): (Example) Estimating Parameters.
1-way fixed-effects ANOVA (part 3/10): Partitioning the Sum of Squares.
1-way fixed-effects ANOVA (part 3/10): (Example) Partitioning the Sum of Squares.
1-way fixed-effects ANOVA (part 4/10): Sum of Squares Derivations.
1-way fixed-effects ANOVA (part 4/10): (Example) Sum of Squares Derivations.
1-way fixed-effects ANOVA (part 5/10): F Test and C.I.'s.
1-way fixed-effects ANOVA (part 5/10): (Example) F Test and C.I.'s.
1-way fixed-effects ANOVA (part 6/10): Unbalanced Case.
1-way fixed-effects ANOVA (part 7/10): Contrasts.
1-way fixed-effects ANOVA (part 7/10): (Example) Contrasts.
1-way fixed-effects ANOVA (part 8/10): Contrasts with Normal Assumptions.
1-way fixed-effects ANOVA (part 8/10): (Example) Contrasts with Normal Assumptions.
1-way fixed-effects ANOVA (part 9/10): Orthogonal Contrasts.
1-way fixed-effects ANOVA (part 9/10): (Example) Orthogonal Contrasts.
1-way fixed-effects ANOVA (part 10/10): Partitioning SS(trt).
1-way fixed-effects ANOVA (part 10/10): (Example) Partitioning SS(trt).
1-way fixed-effects ANOVA (part 11/10): Residuals.
1-way fixed-effects ANOVA (part 11/10): (Example) Residuals.
1-way Random-Effects ANOVA(part 1/6): Model Development.
1-way Random-Effects ANOVA(part 2/6): Distributional Properties of SS.
1-way Random-Effects ANOVA(part 3/6): Another Proof for the Distribution for SS(trt).
1-way Random-Effects ANOVA(part 4/6): Variance Components Estimation.
1-way Random-Effects ANOVA(part 5/6): F Test & C I's.
1-way Random-Effects ANOVA(part 6/6): R Software.
Repeated Measures 1-way fixed effects ANOVA (part 1/7): Model Development.
Repeated Measures 1-way fixed effects ANOVA (part 2/7): Perpendicular Projection Matrices.
Repeated Measures 1-way fixed effects ANOVA (part 3/7): Column Space of the Design Matrix.
Repeated Measures 1-way fixed effects ANOVA (part 4/7): Partitioning the Sum of Squares.
Repeated Measures 1-way fixed effects ANOVA (part 5/7): Distributional Properties of the SS..
Repeated Measures 1-way fixed effects ANOVA (part 6/7): Contrasts.
Repeated Measures 1-way fixed effects ANOVA (part 7/7): R Software Illustrating Parts 1-6.
Randomized Complete Blocks ANOVA (part 1/6): Model Development.
Randomized Complete Blocks ANOVA (part 2/6): Projection Matrices and Column Spaces.
Randomized Complete Blocks ANOVA (part 3/6): Sum of Squares and F-Test.
Randomized Complete Blocks ANOVA (part 4/6): Estimability and Treatment Contrasts.
Randomized Complete Blocks ANOVA (part 5/6): Random Treatment Effects.
Randomized Complete Blocks ANOVA (part 6/6): R Software Illustration.
The Regression Approach to ANOVA (part 1/4): Partial F Test.
The Regression Approach to ANOVA (part 2/4): Type I, II, III, IV Sum of Squares.
The Regression Approach to ANOVA (part 3/4): Balanced Designs.
The Regression Approach to ANOVA (part 4/4): R Software Illustration.
Balanced Incomplete Block Design (part 0/8): Rough Draft.
Balanced Incomplete Block Design (part 1/8): Model Development.
Balanced Incomplete Block Design (part 2/8): Column Spaces of the Design Matrix.
Balanced Incomplete Block Design (part 3/8): Deriving the Least Squares Estimates.
Balanced Incomplete Block Design (part 4/8): Sum of Squares Error and Partial F Test.
Balanced Incomplete Block Design (part 5/8): Notation and Properties for Upcoming Contrast Videos.
Balanced Incomplete Block Design (part 6/8): Estimability and Treatment Contrasts.
Balanced Incomplete Block Design (part 7/8): Partitioning SS(trt) with Orthogonal Contrasts.
Balanced Incomplete Block Design (part 8/8): R Software Illustration.
Analysis of Covariance (part 1/9): Model Development.
Analysis of Covariance (part 2/9): Column Spaces of the Design Matrix.
Analysis of Covariance (part 3/9): Deriving the Least Squares Estimates.
Analysis of Covariance (part 4/9): Sum of Squared Error and Partial F Tests.
Analysis of Covariance (part 5/9): Estimability and Treatment Contrasts.
Analysis of Covariance (part 6/9): Balanced 1-way fixed-effects ANOVA with 1 Covariate.
Analysis of Covariance (part 7/9): Balanced Randomized Complete Block Design ANOVA with 1 Covariate.
Analysis of Covariance (part 8/9): 1-way fixed-effects ANOVA w/ 1covariate.
Analysis of Covariance (part 9/9): 2 Factor ANOVA w/ 2 covariate (NoInteraction).
Balanced 2 Factor Factorial Design without Interaction (part 1/7): Model Development.
Balance 2 Factor Factorial Design without Interaction (part 2/7):Column Spaces of the Design Matrix.
Balanced 2 Factor Factorial Design without Interaction (part 3/7): Partitioning the SS.
Balanced 2 Factor Factorial Design without Interaction (part 4/7): Distribution of Sum of Squares.
Balanced 2 Factor Factorial Design without Interaction (part 5/7): F Tests for Factor Effects.
Balanced 2 Factor Factorial Design without Interaction (part 6/7): Contrasts.
Balanced 2 Factor Factorial Design without Interaction (part 7/7): R Software Illustration.
Balanced 2 Factor Factorial Design with Interaction (part 1/8): Model Development.
Balanced 2 Factor Factorial Design with Interaction (part 2/8): Column Spaces of the Design Matrix.
Balanced 2 Factor Factorial Design with Interaction (part 3/8): Partitioning the SS.
Balanced 2 Factor Factorial Design with Interaction (part 4/8): Distribution of SS and F Tests.
Balanced 2 Factor Factorial Design with Interaction (part 5/8): Contrasts.
Balanced 2 Factor Factorial Design with Interaction (part 6/8): Random Effects Model.
Balanced 2 Factor Factorial Design with Interaction (part 7/8): Random Effects Model F Tests.
Balanced 2 Factor Factorial Design with Interaction (part 8/8): R Software Illustration.
Hierarchical Designs (part 1/11): Model Development.
Hierarchical Designs (part 2/11): Columns Spaces of the Design Matrix.
Hierarchical Designs (part 3/11): Partitioning the SS.
Hierarchical Designs (part 4/11): Distribution of SS and F Tests.
Hierarchical Designs (part 5/11): Contrasts.
Hierarchical Designs (part 6/11): Random Effects.
Hierarchical Designs (part 7/11): Variance Components Estimation.
Hierarchical Designs (part 8/11): 3 Stage Nested.
Hierarchical Designs (part 9/11): Nested and Crossed.
Hierarchical Designs (part 10/11): R Illustration of 2-Stage Nested Design.
Hierarchical Designs (part 11/11): R Illustration of a Nested and Crossed Design.
Split Plot Design (part1/10): Model Development.
Split Plot Design (part 2/10): Design Matrix.
Split Plot Design (part 3/10): Perpendicular Projection Matrices.
Split Plot Design (part 4/10): Column Spaces of the Design Matrix.
Split Plot Design (part 5/10): Best Linear Unbiased Estimate.
Split Plot Design (part 6/10): Partitioning the Total SS.
Split Plot Design (part 7/10): Expected SS.
Split Plot Design (part 8/10): Distribution of SS.
Split Plot Design (part 9/10): F Tests.
Split Plot Design (part 10/10): R Illustration / Example.

(Please note that we obtained the following content based on information that users may want to know, such as skills, applicable scenarios, future development, etc., combined with AI tools, and have been manually reviewed)

Design of Experiments: Models Introduction.
Design of Experiments: Projection Matrix onto c(X).
Design of Experiments: Projection Matrix onto c(X) Example.
Design of Experiments: Least Square Estimator of Beta.
Estimability (part 1/4): Necessary and Sufficient Conditions.
Estimability (part 2/4): Unique Unbiased Estimator.
Estimability (part 3/4): Gauss Markov Theorem.
Estimability (part 4/4): Generating Estimable Functions.
Design of Experiments: Estimating the Error Variance.
1-way fixed-effects ANOVA (part 1/10): Model Development.
1-way fixed-effects ANOVA (part 1/10): (Example) Model Development.
1-way fixed-effects ANOVA (part 2/10): Estimating Parameters.
1-way fixed-effects ANOVA (part 2/10): (Example) Estimating Parameters.
1-way fixed-effects ANOVA (part 3/10): Partitioning the Sum of Squares.
1-way fixed-effects ANOVA (part 3/10): (Example) Partitioning the Sum of Squares.
1-way fixed-effects ANOVA (part 4/10): Sum of Squares Derivations.
1-way fixed-effects ANOVA (part 4/10): (Example) Sum of Squares Derivations.
1-way fixed-effects ANOVA (part 5/10): F Test and C.I.'s.
1-way fixed-effects ANOVA (part 5/10): (Example) F Test and C.I.'s.
1-way fixed-effects ANOVA (part 6/10): Unbalanced Case.
1-way fixed-effects ANOVA (part 7/10): Contrasts.
1-way fixed-effects ANOVA (part 7/10): (Example) Contrasts.
1-way fixed-effects ANOVA (part 8/10): Contrasts with Normal Assumptions.
1-way fixed-effects ANOVA (part 8/10): (Example) Contrasts with Normal Assumptions.
1-way fixed-effects ANOVA (part 9/10): Orthogonal Contrasts.
1-way fixed-effects ANOVA (part 9/10): (Example) Orthogonal Contrasts.
1-way fixed-effects ANOVA (part 10/10): Partitioning SS(trt).
1-way fixed-effects ANOVA (part 10/10): (Example) Partitioning SS(trt).
1-way fixed-effects ANOVA (part 11/10): Residuals.
1-way fixed-effects ANOVA (part 11/10): (Example) Residuals.
1-way Random-Effects ANOVA(part 1/6): Model Development.
1-way Random-Effects ANOVA(part 2/6): Distributional Properties of SS.
1-way Random-Effects ANOVA(part 3/6): Another Proof for the Distribution for SS(trt).
1-way Random-Effects ANOVA(part 4/6): Variance Components Estimation.
1-way Random-Effects ANOVA(part 5/6): F Test & C I's.
1-way Random-Effects ANOVA(part 6/6): R Software.
Repeated Measures 1-way fixed effects ANOVA (part 1/7): Model Development.
Repeated Measures 1-way fixed effects ANOVA (part 2/7): Perpendicular Projection Matrices.
Repeated Measures 1-way fixed effects ANOVA (part 3/7): Column Space of the Design Matrix.
Repeated Measures 1-way fixed effects ANOVA (part 4/7): Partitioning the Sum of Squares.
Repeated Measures 1-way fixed effects ANOVA (part 5/7): Distributional Properties of the SS..
Repeated Measures 1-way fixed effects ANOVA (part 6/7): Contrasts.
Repeated Measures 1-way fixed effects ANOVA (part 7/7): R Software Illustrating Parts 1-6.
Randomized Complete Blocks ANOVA (part 1/6): Model Development.
Randomized Complete Blocks ANOVA (part 2/6): Projection Matrices and Column Spaces.
Randomized Complete Blocks ANOVA (part 3/6): Sum of Squares and F-Test.
Randomized Complete Blocks ANOVA (part 4/6): Estimability and Treatment Contrasts.
Randomized Complete Blocks ANOVA (part 5/6): Random Treatment Effects.
Randomized Complete Blocks ANOVA (part 6/6): R Software Illustration.
The Regression Approach to ANOVA (part 1/4): Partial F Test.
The Regression Approach to ANOVA (part 2/4): Type I, II, III, IV Sum of Squares.
The Regression Approach to ANOVA (part 3/4): Balanced Designs.
The Regression Approach to ANOVA (part 4/4): R Software Illustration.
Balanced Incomplete Block Design (part 0/8): Rough Draft.
Balanced Incomplete Block Design (part 1/8): Model Development.
Balanced Incomplete Block Design (part 2/8): Column Spaces of the Design Matrix.
Balanced Incomplete Block Design (part 3/8): Deriving the Least Squares Estimates.
Balanced Incomplete Block Design (part 4/8): Sum of Squares Error and Partial F Test.
Balanced Incomplete Block Design (part 5/8): Notation and Properties for Upcoming Contrast Videos.
Balanced Incomplete Block Design (part 6/8): Estimability and Treatment Contrasts.
Balanced Incomplete Block Design (part 7/8): Partitioning SS(trt) with Orthogonal Contrasts.
Balanced Incomplete Block Design (part 8/8): R Software Illustration.
Analysis of Covariance (part 1/9): Model Development.
Analysis of Covariance (part 2/9): Column Spaces of the Design Matrix.
Analysis of Covariance (part 3/9): Deriving the Least Squares Estimates.
Analysis of Covariance (part 4/9): Sum of Squared Error and Partial F Tests.
Analysis of Covariance (part 5/9): Estimability and Treatment Contrasts.
Analysis of Covariance (part 6/9): Balanced 1-way fixed-effects ANOVA with 1 Covariate.
Analysis of Covariance (part 7/9): Balanced Randomized Complete Block Design ANOVA with 1 Covariate.
Analysis of Covariance (part 8/9): 1-way fixed-effects ANOVA w/ 1covariate.
Analysis of Covariance (part 9/9): 2 Factor ANOVA w/ 2 covariate (NoInteraction).
Balanced 2 Factor Factorial Design without Interaction (part 1/7): Model Development.
Balance 2 Factor Factorial Design without Interaction (part 2/7):Column Spaces of the Design Matrix.
Balanced 2 Factor Factorial Design without Interaction (part 3/7): Partitioning the SS.
Balanced 2 Factor Factorial Design without Interaction (part 4/7): Distribution of Sum of Squares.
Balanced 2 Factor Factorial Design without Interaction (part 5/7): F Tests for Factor Effects.
Balanced 2 Factor Factorial Design without Interaction (part 6/7): Contrasts.
Balanced 2 Factor Factorial Design without Interaction (part 7/7): R Software Illustration.
Balanced 2 Factor Factorial Design with Interaction (part 1/8): Model Development.
Balanced 2 Factor Factorial Design with Interaction (part 2/8): Column Spaces of the Design Matrix.
Balanced 2 Factor Factorial Design with Interaction (part 3/8): Partitioning the SS.
Balanced 2 Factor Factorial Design with Interaction (part 4/8): Distribution of SS and F Tests.
Balanced 2 Factor Factorial Design with Interaction (part 5/8): Contrasts.
Balanced 2 Factor Factorial Design with Interaction (part 6/8): Random Effects Model.
Balanced 2 Factor Factorial Design with Interaction (part 7/8): Random Effects Model F Tests.
Balanced 2 Factor Factorial Design with Interaction (part 8/8): R Software Illustration.
Hierarchical Designs (part 1/11): Model Development.
Hierarchical Designs (part 2/11): Columns Spaces of the Design Matrix.
Hierarchical Designs (part 3/11): Partitioning the SS.
Hierarchical Designs (part 4/11): Distribution of SS and F Tests.
Hierarchical Designs (part 5/11): Contrasts.
Hierarchical Designs (part 6/11): Random Effects.
Hierarchical Designs (part 7/11): Variance Components Estimation.
Hierarchical Designs (part 8/11): 3 Stage Nested.
Hierarchical Designs (part 9/11): Nested and Crossed.
Hierarchical Designs (part 10/11): R Illustration of 2-Stage Nested Design.
Hierarchical Designs (part 11/11): R Illustration of a Nested and Crossed Design.
Split Plot Design (part1/10): Model Development.
Split Plot Design (part 2/10): Design Matrix.
Split Plot Design (part 3/10): Perpendicular Projection Matrices.
Split Plot Design (part 4/10): Column Spaces of the Design Matrix.
Split Plot Design (part 5/10): Best Linear Unbiased Estimate.
Split Plot Design (part 6/10): Partitioning the Total SS.
Split Plot Design (part 7/10): Expected SS.
Split Plot Design (part 8/10): Distribution of SS.
Split Plot Design (part 9/10): F Tests.
Split Plot Design (part 10/10): R Illustration / Example.

Course Provider

Provider Youtube's Stats at AZClass

Discussion and Reviews

0.0   (Based on 0 reviews)

Start your review of General Linear Models: Design of Experiments

Explore Similar Online Courses

Hairstyles 101: Draw and Colour Hair for Character Design

Hairstyles 101: Draw and Colour Hair for Character Design
Space Rocks! - A complete game in Godot Game Engine

Space Rocks! - A complete game in Godot Game Engine
Python for Informatics: Exploring Information

Python for Informatics: Exploring Information
Social Network Analysis

Social Network Analysis
Introduction to Systematic Review and Meta-Analysis

Introduction to Systematic Review and Meta-Analysis
The Analytics Edge

The Analytics Edge
DCO042 - Python For Informatics

DCO042 - Python For Informatics
Causal Diagrams: Draw Your Assumptions Before Your Conclusions

Causal Diagrams: Draw Your Assumptions Before Your Conclusions
Whole genome sequencing of bacterial genomes - tools and applications

Whole genome sequencing of bacterial genomes - tools and applications
Data Science: Linear Regression

Data Science: Linear Regression
Simple Linear Regression for the Absolute Beginner

Simple Linear Regression for the Absolute Beginner
Linear Regression and Linear Models

Linear Regression and Linear Models

Related Categories Related Categories

Multivariable Calculus hot Algebra hot Calculus hot Geometry Linear Algebra Linear Programming Trigonometry Number Theory Statistics & Probability Business Calculus

Popular Providers Popular Providers

Scrimba Qwiklabs Domestika Udacity Masterclass

Popular Searches Popular Searches

YouTube History Courses YouTube Video Editing Courses YouTube Yoga Courses YouTube SEO Courses YouTube Customer Service Courses YouTube Drawing Courses Coursera Spanish Courses YouTube Welding Courses freeCodeCamp Kotlin Courses YouTube Music Theory Courses

faq FAQ for Linear Regression Courses

Q1: Does the course offer certificates upon completion?

Yes, this course offers a free certificate. AZ Class have already checked the course certification options for you. Access the class for more details.

Q2: How do I contact your customer support team for more information?

If you have questions about the course content or need help, you can contact us through "Contact Us" at the bottom of the page.

Q3: Can I take this course for free?

Yes, this is a free course offered by Youtube, please click the "go to class" button to access more details.

Q4: How many people have enrolled in this course?

So far, a total of 0 people have participated in this course. The duration of this course is 22.00 hour(s). Please arrange it according to your own time.

Q5: How Do I Enroll in This Course?

Click the"Go to class" button, then you will arrive at the course detail page.
Watch the video preview to understand the course content.
(Please note that the following steps should be performed on Youtube's official site.)
Find the course description and syllabus for detailed information.
Explore teacher profiles and student reviews.
Add your desired course to your cart.
If you don't have an account yet, sign up while in the cart, and you can start the course immediately.
Once in the cart, select the course you want and click "Enroll."
Youtube may offer a Personal Plan subscription option as well. If the course is part of a subscription, you'll find the option to enroll in the subscription on the course landing page.
If you're looking for additional Linear Regression courses and certifications, our extensive collection at azclass.net will help you.

close

To provide you with the best possible user experience, we use cookies. By clicking 'accept', you consent to the use of cookies in accordance with our Privacy Policy.